Numerical Examples

This page illustrates how FsRandom is applicable to scientific computations. For statistics, the Statistics module is useful:

1: 

open FsRandom.Statistics

Estimating pi, the ratio of a circle's circumference to its diameter

Suppose there is a circle of radius 1 is inside a square with side length 2. The area of the circle is \(\pi\) and the area of the square is 4. If you put \(N\) random points on the square, roughly \(\displaystyle\frac{\pi}{4}N\) points are inside the circle. In other words, if you find \(M\) points out of \(N\) are inside the circle, \(\displaystyle\frac{M}{N}\) approximates \(\displaystyle\frac{\pi}{4}\).

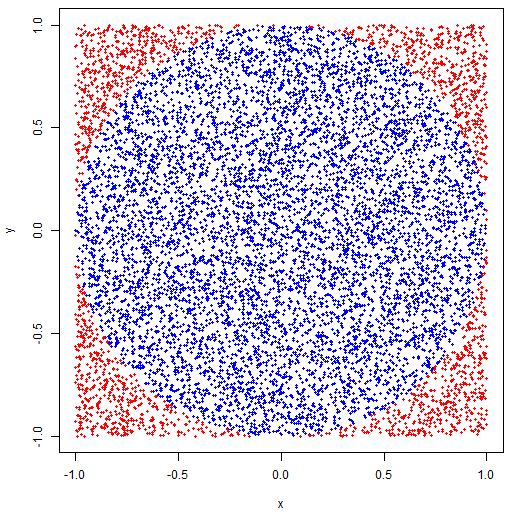
Random points can be described simply and easily as follows:

1: 
2: 
3: 
4: 
5: 

let randomPointGenerator = random {
   let! x = uniform (-1.0, 1.0)
   let! y = uniform (-1.0, 1.0)
   return (x, y)
}

To give each point weight 4 if the point is inside the circle and 0 otherwise adjusts the average of total score to become \(\pi\).

1: 
2: 

let weight (x, y) = if x * x + y * y <= 1.0 then 4.0 else 0.0
let randomScoreGenerator = Random.map weight randomPointGenerator

The average of the random scores approximates \(\pi\). To generate 1,000,000 scores and to compute the approximation:

1: 
2: 
3: 
4: 

Seq.ofRandom randomScoreGenerator state
|> Seq.take 1000000
|> Seq.average
|> printf "%f"

3.140812

Generating bivariate normal random numbers using Gibbs sampler

To sample from bivariate normal distribution \(\displaystyle N_{2}\left( \left[\begin{array}{c} \mu_{X} \\ \mu_{Y} \end{array}\right], \left[\begin{array}{cc} \sigma_{X}^{2} & \sigma_{XY} \\ \sigma_{XY} & \sigma_{Y}^{2} \end{array}\right] \right) \), you will construct a Gibbs sampler. Let \(f_{2}(x, y)\) be the density function of \(N_{2}\), and let \(x'\) and \(y'\) be \(x-\mu_{X}\) and \(y-\mu_{Y}\) respectively. Then, \[\begin{eqnarray} f\_{2}(x, y) & \propto & \exp\left( -\frac{1}{2}\left[\begin{array}{c} x' \\\\ y' \end{array}\right]^{T} \left[\begin{array}{cc} \sigma\_{X}^{2} & \sigma\_{XY} \\\\ \sigma\_{XY} & \sigma\_{Y}^{2} \end{array}\right]^{-1} \left[\begin{array}{c} x' \\\\ y' \end{array}\right] \right) \\\\ & \propto & \exp\left( -\frac{\left(x'-\sigma\_{XY}y'/\sigma\_{Y}^{2}\right)^{2}}{2\left(\sigma\_{X}^{2}-\sigma\_{XY}^{2}/\sigma\_{Y}^{2}\right)} \right) \end{eqnarray}\] This means the conditional probability of \(x\) given \(y\) is distributed normally, and its mean is \(\displaystyle \mu_{X}+\frac{\sigma_{XY}}{\sigma_{Y}^{2}}\left(y-\mu_{Y}\right)\) and its variance is \(\displaystyle \sigma_{X}^{2}-\frac{\sigma_{XY}^{2}}{\sigma_{Y}^{2}}\). Therefore, the Gibbs sampler for bivariate normal distribution consists of iterating as the following:

1. Draw \(\displaystyle x_{t+1}\sim N\left(\mu_{X}+\frac{\sigma_{XY}}{\sigma_{Y}^{2}}(y_{t}-\mu_{Y}), \sigma_{X}^{2}-\frac{\sigma_{XY}^{2}}{\sigma_{Y}^{2}}\right)\)
2. Draw \(\displaystyle y_{t+1}\sim N\left(\mu_{Y}+\frac{\sigma_{XY}}{\sigma_{X}^{2}}(x_{t+1}-\mu_{Y}), \sigma_{Y}^{2}-\frac{\sigma_{XY}^{2}}{\sigma_{X}^{2}}\right)\)

And it can be naturally translated into F# code as the following.

1: 
2: 
3: 
4: 
5: 
6: 
7: 
8: 
9: 

let gibbsBinormal (meanX, meanY, varX, varY, cov) =
   let sdx = sqrt <| varX - cov ** 2.0 / varY
   let sdy = sqrt <| varY - cov ** 2.0 / varX
   fun (_, y) -> random {
      let! x' = normal (meanX + cov * (y - meanY) / varY, sdx)
      let! y' = normal (meanY + cov * (x' - meanX) / varX, sdy)
      return (x', y')
   }
let binormal parameter = Seq.markovChain (gibbsBinormal parameter)

Note that the generating bivariate normal random number sequence is autocorrelated.

Hamiltonian Monte Carlo

Gibbs sampler sometimes produces strongly autocorrelated traces. Hamiltonian Monte Carlo (also known as hybrid Monte Carlo) could be efficient in such situations. Hamiltonian Monte Carlo algorithm is available if you know about the density of the taget distribution without normalizing constant.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 
23: 
24: 
25: 
26: 
27: 
28: 
29: 
30: 
31: 
32: 

let inline updateWith f (ys:float []) (xs:float []) =
   for index = 0 to Array.length xs - 1 do
      xs.[index] <- f xs.[index] ys.[index]

/// Hamiltonian Monte Carlo
let hmc minusLogDensity gradMinusLogDensity epsilon step =
   /// Leapfrog integration
   let leapfrog q p =
      updateWith (fun x y -> x + 0.5 * epsilon * y) (gradMinusLogDensity q) p
      for i = 1 to step - 1 do
         updateWith (fun x y -> x + epsilon * y) p q
         updateWith (fun x y -> x - epsilon * y) (gradMinusLogDensity q) p
      updateWith (fun x y -> x + epsilon * y) p q
      updateWith (fun x y -> -x + 0.5 * epsilon * y) (gradMinusLogDensity q) p
   /// Hamiltonian
   let hamiltonian q p =
      let potential = minusLogDensity q
      let kinetic = Array.fold (fun acc x -> acc + x * x) 0.0 p / 2.0
      potential + kinetic
   /// resampling of particles
   let resampleK n = Array.randomCreate n Standard.normal
   fun currentQ -> random {
      let q = Array.copy currentQ
      // resampling of particles
      let! currentP = resampleK (Array.length currentQ)
      let p = Array.copy currentP
      leapfrog q p
      let currentH = hamiltonian currentQ currentP
      let proposedH = hamiltonian q p
      let! r = ``[0, 1)``
      return if r < exp (currentH - proposedH) then q else currentQ
   }

Approximate Bayesian Computation

Approximate Bayesian computation is known as a likelihood-free method of parameter estimation. This section follows the example in the Wikipedia article.

The initial state of the system is not described whether it is determined or inferred. Here it is assumed as 'A' for convenience. Then, the model is described as follows:

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 

type HiddenSystem = A | B
let switch = function A -> B | B -> A
let observe correctly = function
   | A -> if correctly then 'A' else 'B'
   | B -> if correctly then 'B' else 'A'
let model (theta, gamma, length) = random {
   let state = ref A
   let builder = System.Text.StringBuilder ()
   for index = 1 to length do
      let! switchState = Utility.flipCoin theta
      if switchState then state := switch !state
      let! correctly = Utility.flipCoin gamma
      builder.Append (observe correctly !state) |> ignore
   return builder.ToString ()
}

Step 1: the observed data is AAAABAABBAAAAAABAAAA.

1: 

let observed = "AAAABAABBAAAAAABAAAA"

Step 2: the prior of theta is a uniform [0, 1] and gamma is known.

1: 
2: 

let prior = uniform (0.0, 1.0)
let gamma = 0.8

Step 3: the summary statistic is the frequency of switches between two states (A and B). Note that the summary statistic is bad to estimate theta (see the article).

1: 
2: 
3: 
4: 

let w (data:string) =
   Seq.windowed 2 data
   |> Seq.filter (fun c -> c.[0] <> c.[1])  // switch
   |> Seq.length

Step 4: the distance between the observed and simulated is the difference between the summary statistics.

1: 

let rho simulated = abs (w observed - w simulated)

Step 5: do the simulation with tolerance epsilon.

1: 
2: 
3: 
4: 
5: 
6: 
7: 
8: 

type SimulationResult =
   | Accept of float
   | Reject
let simulate epsilon = random {
   let! theta = prior
   let! simulated = model (theta, gamma, String.length observed)
   return if rho simulated <= epsilon then Accept (theta) else Reject
}

• FsRandom
• Home page
• Get Library via NuGet
• Source Code on GitHub
• License (BSD 3-clause)
• Change Log
• Documentation
• First random number
• Transforming random numbers
• Random Number Sequence
• Generator function
• Pseudo-random number generator
• API Reference
• Using From C#
• Numerical Examples
• Estimating pi
• Gibbs sampler
• Hamiltonian Monte Carlo
• Approximate Bayesian Computation